ターレスの定理、タレースの定理ともいう 歴史編集 古代ギリシャの哲学者、数学者 タレスにちなんで名付けられた その前にもこの定理は発見されていたが、タレスが初めてピラミッドの高さを発見した事からこの名前が生まれた円周角の定理においては、「ある1点から円周上の2点に直線を伸ばす」という表現からわかるように、3つの点が登場します。 円周角の定理の逆や、いろいろな応用問題もあわせて解説。 《証明》 ・二等辺三角形を使う ・ターレスの定理を使う ・円周角の ユキムから、Thales Tonarm(ターレス・トーンアーム)の新製品「THALES STATEMENT」が発表された。有効長230mm、ストレートタイプのトーンアームで、価格は¥2,400,000(税別)。受注生産で、今年9月から注文を受け付ける。 ターレス・トーンアームは、スイスのチューリッヒ州ヴィンタートゥールに

中学数学 中学流 に外接円の半径を求める ジャムと愉快な仲間たち 0名
ターレス の 定理
ターレス の 定理-ターレスの定理 以前、入試の採点をしているとき、「ターレスの定理より、・・・」と論述している受験生の答 案があり、採点官の間でしばし話題になった。 ターレス(BC624頃~BC548頃)は、現在のトルコにあるミレトス出身の数学者であり哲学 者で、定理を提唱し、それを証明するという抽象数学の元祖と言われる。 その頃、日本は弥 生時代で、ターレスこれを「タレース(タレス、ターレス)の定理」と言います。 「タレースの定理」はこれだけでなく、「対頂角は等しい」「二等辺三角形 の底角は等しい」など5~6個の定理を指します。 今では当たり前のことば かりですが、紀元前6世紀ころのことです。




ユークリッド幾何学 Ja Wikitechpro Com
練習プリントをダウンロード https//ecommonsbiz/wpcontent/uploads//11/DB1172pdf 動画リンク おうぎ形まとめ https//youtube/DpgfxZEiyjoタレスの定理 (タレスのていり、 英 Thales' theorem )とは、直径に対する円周角は直角である、つまり、A, B, C が円周上の相異なる 3 点で、線分 AC が直径であるとき、∠ABC が直角であるという定理である。 ターレスの定理 、 タレースの定理 ともいう。ファンレターやプレゼントの宛先はこちら 〒 東京都目黒区青葉台3628 住友不動産青葉台タワー2F 株式会社Kiii AKITO宛 ※冷蔵・冷凍が必要な
定理 $\textcolor{blue}{2}$ :$\textcolor{blue}{1}$ つの弧に対する円周角はすべて等しい $\rm ∠AQB=∠APB=∠ARB$ (すべて $\stackrel{\frown}{\rm AB}$ に対する円周角) 1:10タレスの定理(タレスのていり、英 Thales' theorem )とは、直径に対する円周角は直角である、つまり、A, B, C が円周上の相異なる 3 点で、線分 AC が直径であるとき、∠ABC が直角であるという定理である。 ターレスの定理、タレースの定理ともいう。 歴史 古代ギリシャの哲学者、数学者ターレス :①ピラミッドの影の長さを測ってピラミッドの高さを求め る. ②直径に対する円周角は直角(ターレスの定理). ③任意の二つの三角形で,1辺とその両端の角が等しいとき, その三角形は合になること を発見.
タレスの定理(タレスのていり、英 Thales' theorem )とは、直径に対する円周角は直角である、つまり、A, B, C が円周上の相異なる 3 点で、線分 AC が直径であるとき、∠ABC が直角であるという定理である。 ターレスの定理、タレースの定理ともいう。 歴史例えば、ターレスは対頂角が等しいことを次のように証明した。 (1) aとbが等しいことを説明する。 (2) そのために第三項cを考える。 (3) a+c=180°(直線は180°) b+c=180° 発問51 ターレスの証明のReed 5Aは、バーチジオメトリをダブルで使用する独自の「ダブルバーチジオメトリ」と、Reed 5Tにも採用されているターレスの定理を融合させた、画期的なトーンアームです。 右がこの原理を忠実に再現するReed5Aの原理図です。 P1, O1, P3ターレスの半円 角P1




月食が教えてくれる大地の形 あんなこと こんなこと 京からの独り言




円周角の定理と羽根を広げた蝶 デザインtシャツ通販 Tシャツトリニティ
アインシュタインの特殊相対性理論が、このターレスの定理を使って説明してあります。 (ct) 2 =(vt) 2 +S 2 (cは光りの速さ、tは時間、vは物体の速さ、Sは時空間隔)と表すと、これまたターレスの定理を使ってSを表すことができるのです。定理一覧 円を含む図形 方べきの定理 トレミーの定理 シムソンの定理 シュタイナーの定理 アルハゼンの定理 ニュートンの定理 九点円の定理 フォイエルバッハの定理 ターレスの定理 パスカルの定理 アポロニウスの定理 ブリアンショの定理ターレスの定理の逆 Thales' theorem ターレスの定理の逆・・・ターレスの定理はいろいろ役に立ちます。 (斜面の落体の速度、特殊相対論など)



Xp9ax13dult21c0wtxqar30g7ld Com Nagasaki Sugaku H30 Q3



パースのかかった円の描き方 デジタル限定 Remi S Essay
ターレスの定理に基づいた革新的再生メカニズム 三角形の外接円の中心が三角形上にある場合、その三角形は直角三角形であり直径に対する円周角は、直角である 右がこの原理を忠実に再現するReed5Tの原理図です。 P1, O1, P3ターレスの半円三角形のターレスの定理をもとに考案されたTHALES(ターレス)と違い、Simplicityは四角形のテトラゴン・ソリューションをアイデアの基本としています。 そして14年。 初代のSimplicityをさらに進化させたThales Tonarmの最上位モデルとなるtype 2が完成しました。ターレスの定理 の用例・例文集 一般の人によく知られているのは哲学よりも、中学校の数学の教科書に必ず出てくるターレスの定理であろう。ちなみに「ターレスの定理」とよばれるものは5つある。ターレスの定理、タレースの定理ともいう。




High End Audio ページ 3 Eilex




中学数学 中学流 に外接円の半径を求める ジャムと愉快な仲間たち 0名
ピタゴラスの定理 ピタゴラスの定理の証明 この定理には数百通りもの異なる証明があり、例えば、「以下では頂点 a, b, c からなる三角形を abc と表す」「各辺 ab, bc, ca に向かい合う角をタレスの定理(タレスのていり、英 Thales' theorem )とは、直径に対する円周角は直角である、つまり、A, B, C が円周上の相異なる 3 点で、線分 AC が直径であるとき、∠ABC が直角であるという定理である。 ターレスの定理、タレースの定理ともいう。 歴史 古代ギリシャの哲学者、数学者タレス タレスの定理の逆を証明する。 すなわち、∠cを直角とする直角三角形abcと、頂点abcを通る円を考えるとき、図のように辺abが円の直径になることを示す。 証明 辺abの中点をpとし、点pから∠cに補助線を引く。 pcと平行に点aから新たな補助線を引く。




未分類 Rkernel



3




Reed リードのご紹介



初心者向け 三角関数と指数 対数関数の 巡回性 について Qiita



Xp9ax13dult21c0wtxqar30g7ld Com Nagasaki Sugaku H30 Q3




コレクション 四角形 の 角度 Uyenblogwallji



タレスの定理 の宇宙




当然の定義 単語 21




Twigacandle




Category Thales Theorem Wikimedia Commons
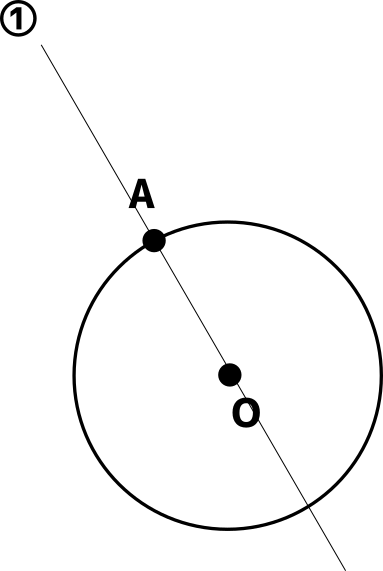



70以上 接線 の 作図
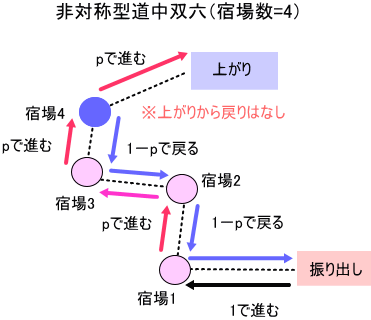



マルコフ過程 6 非対称型道中双六 平均日数と対称式




印刷可能 ターレス 画像 人気の画像を無料でダウンロード




コレクション 四角形 の 角度 Uyenblogwallji




ターレス




地球と天体そして宇宙 発見 発明の歴史図鑑 アニメおやじブログ



数学の図形問題アプリeuclideaレビュー この界隈を散歩中




中学数学 中学流 に外接円の半径を求める ジャムと愉快な仲間たち 0名



1




ユークリッド幾何学 Ja Wikitechpro Com




中等教育前期の数学 幾何編 下巻 円 Wikibooks
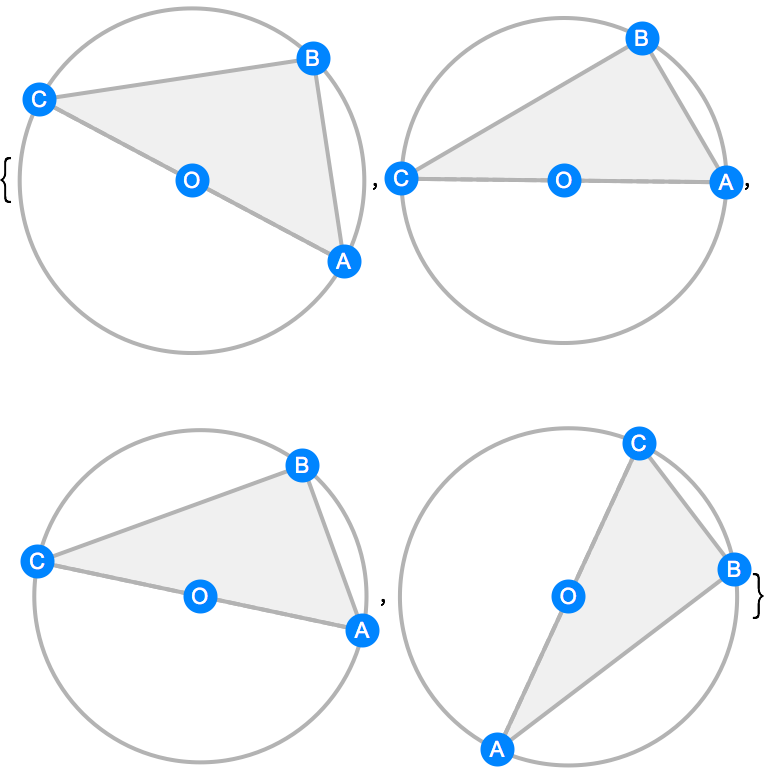



簡単な予想を求める タレス Thales の定理 Wolfram言語 12の新機能




円 数学 Wikipedia



投稿192



Maths 3eme Annee College الثالثة إعدادي خيار فرنسي Google Play のアプリ




Vertical 垂直 Wikipe Wiki




タレスと




書評 ピタゴラスの定理



九点円 Wolfram言語 12の新機能




52 数値積分 1 台形公式とベルヌイ数



回帰分析について 渋谷のaiメンターのブログ




17 02 28 火 自然哲学者タレスのお話 霊観占 大幸 れいかんうらない だいこう




中学数学 中学流 に外接円の半径を求める ジャムと愉快な仲間たち 0名




Category Thales Theorem Wikimedia Commons




Reed 5t Eilex




Intercept Theorem Wikipedia



回帰分析について 渋谷のaiメンターのブログ



Rで球面幾何学 そもそも 内積 Inner Product とは 外積 Outer Product とは何か Qiita
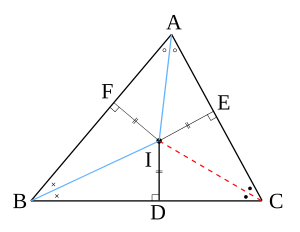



中等教育前期の数学 幾何編 下巻 円 Wikibooks




中学数学 中学流 に外接円の半径を求める ジャムと愉快な仲間たち 0名




円周角の定理はこれで完璧 定理の証明と様々な問題の解法



幾何学 Wikipedia
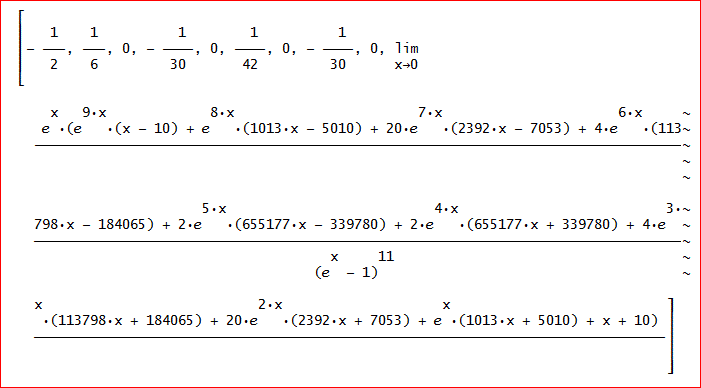



52 数値積分 1 台形公式とベルヌイ数




当然の定義 単語 21




明日に向かって走れ 大工さんの数学 さしがね 曲尺



射影幾何学 グラフィック表現




Images Of 高木の存在定理 Japaneseclass Jp




中等教育前期の数学 幾何編 下巻 円 Wikibooks




タレス ターレスの似顔絵イラスト かわいいフリー素材集 いらすとや




タレス タレース 古希 8alhs 希 Thales 紀元前624年頃 紀元前546年頃 Institute Of Reproducing Kernels




書評 ピタゴラスの定理




中等教育前期の数学 幾何編 下巻 円 Wikibooks
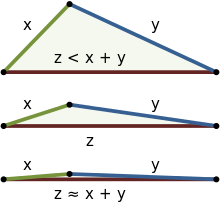



初心者向け 三角不等式 Triangle Inequality の体感方法 Qiita
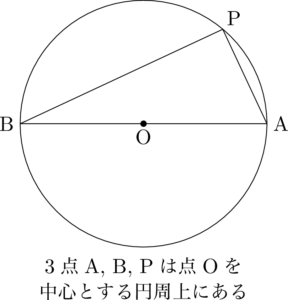



3点を通る円の方程式を簡単に求める方法とは ページ 3 大学入試数学の考え方と解法




中等教育前期の数学 幾何編 下巻 円 Wikibooks



幾何学 Google Play のアプリ



Rで射影幾何学 それでは 射影 とは何か Qiita




中等教育前期の数学 幾何編 下巻 円 Wikibooks




課題学習の指導 数学
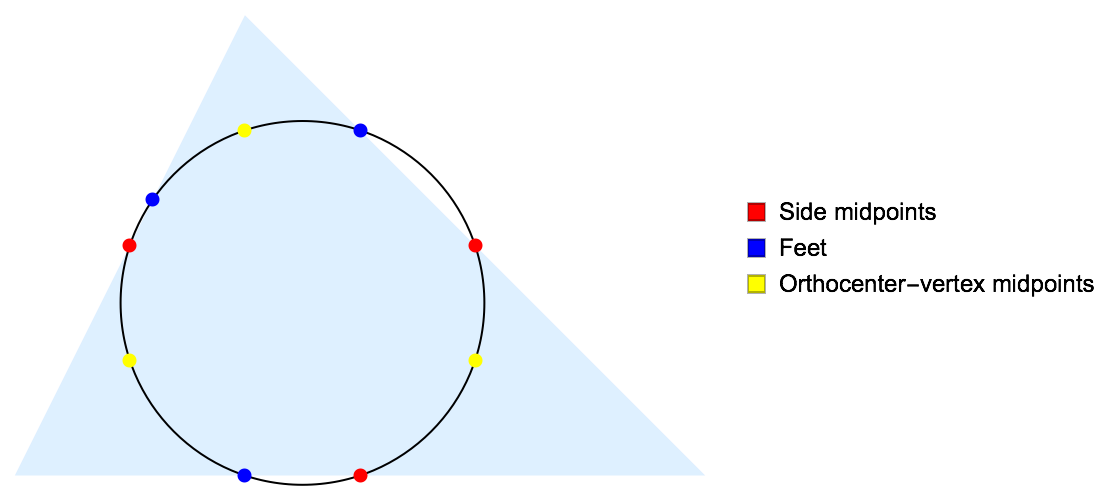



九点円 Wolfram言語 12の新機能




ターレス



数学者のいう数学の美しさとはなんなのですか Quora
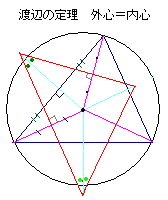



米倉の定理
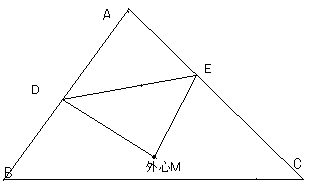



米倉の定理




円周角の定理




パース理論の完全形態 透視図法解剖図 お絵描きホーホー論 Note



射影幾何学 グラフィック表現




Category Thales Theorem Wikimedia Commons



楕円傾き計算について正円を傾けると楕円に見えます その楕円の長軸 Yahoo 知恵袋




円 数学 Wikiwand



回帰分析について 渋谷のaiメンターのブログ
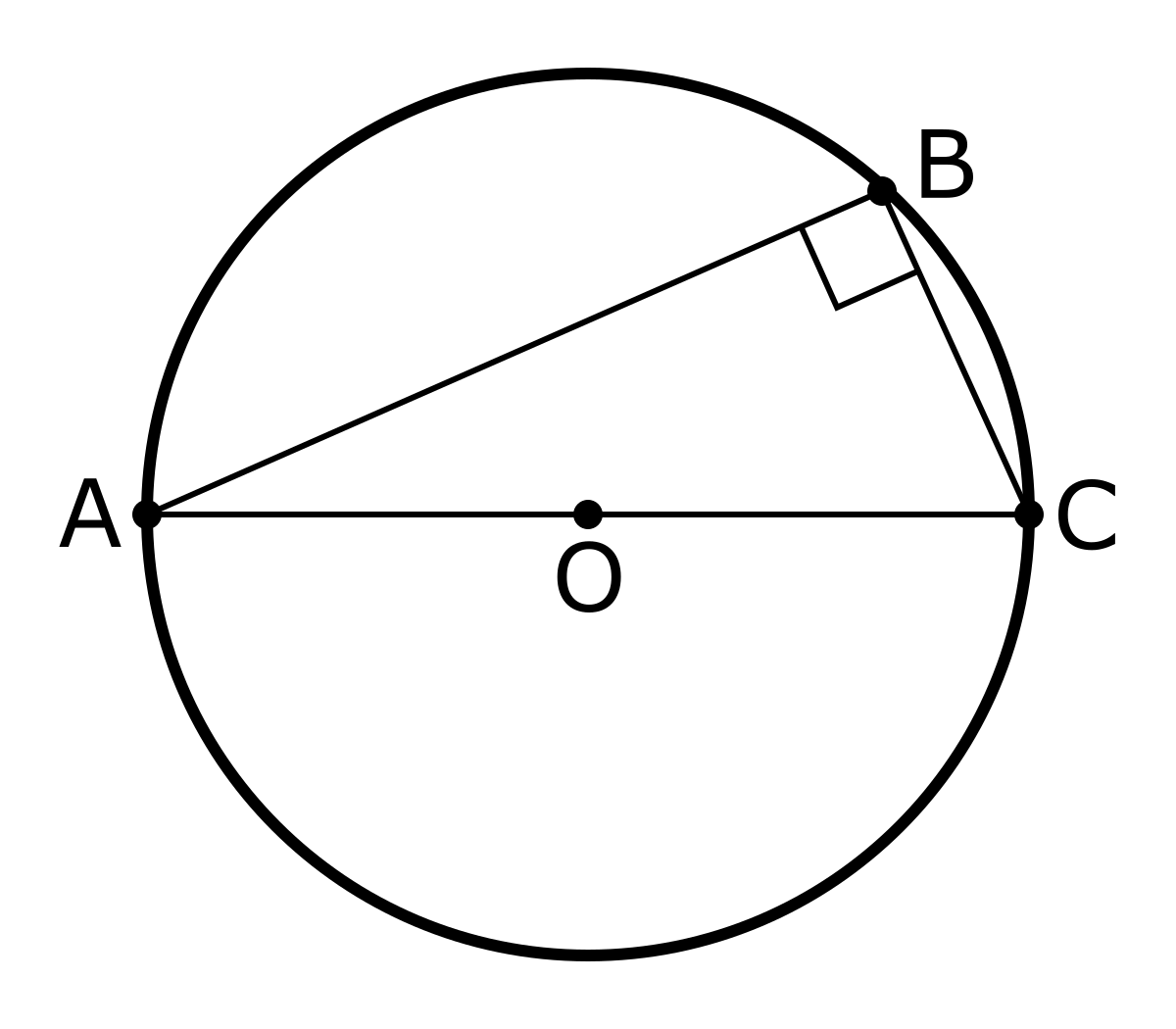



タレスの定理 Wikipedia



1




地球と天体そして宇宙 発見 発明の歴史図鑑 アニメおやじブログ




書評 ピタゴラスの定理




基本 円の方程式 なかけんの数学ノート



円周角の定理は中学何年生でならいますか 学習指導要領が変わったので 中 Yahoo 知恵袋




ユークリッド幾何学 Ja Wikitechpro Com
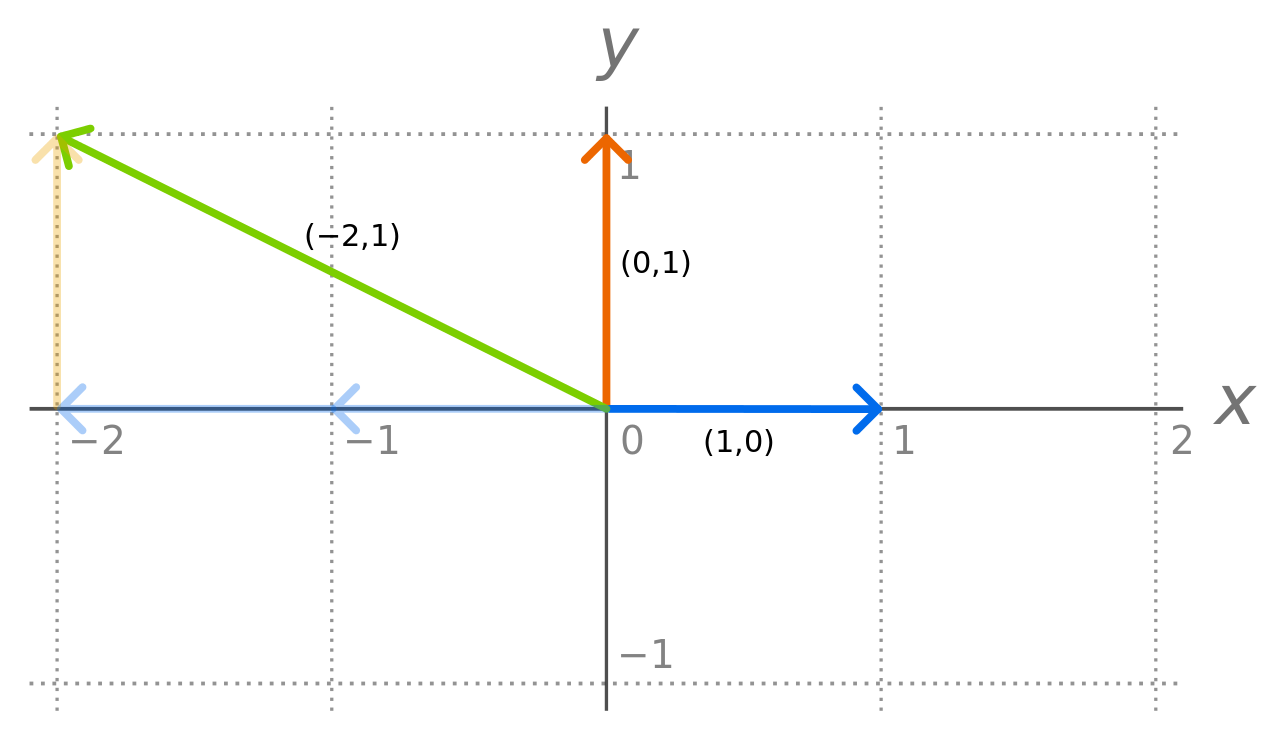



Rで射影幾何学 それでは 射影 とは何か Qiita




ターレス




論理的思考を社会科の倫理から学ぶ タレスを例に解説 勉強法の大辞典 ベンテン




四角形 の 角度



1




論理的思考を社会科の倫理から学ぶ タレスを例に解説 勉強法の大辞典 ベンテン
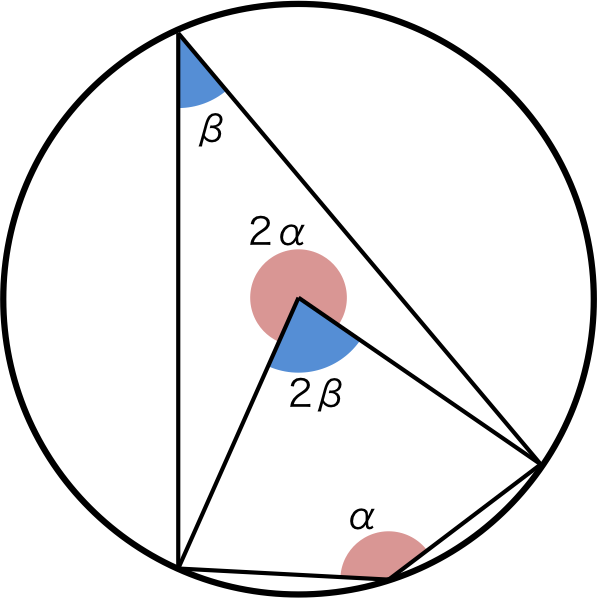



円 三角形 角度 定理 円 三角形 角度 定理




古代に始まったその当時の常識にない思想とソフィストとの闘いとは 人生は楽しい




円 数学 Wikipedia
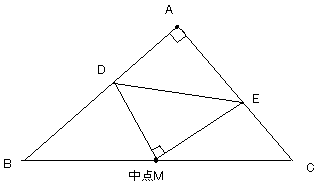



米倉の定理




タレス ターレスの似顔絵イラスト かわいいフリー素材集 いらすとや




書評 ピタゴラスの定理




円 数学 Wikiwand
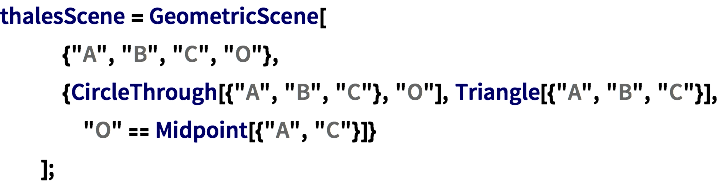



簡単な予想を求める タレス Thales の定理 Wolfram言語 12の新機能



難関大学 数学の発想のしかた さくら教育研究所 Skredu 23ページ目



Xp9ax13dult21c0wtxqar30g7ld Com Nagasaki Sugaku H30 Q3




中学数学 中学流 に外接円の半径を求める ジャムと愉快な仲間たち 0名
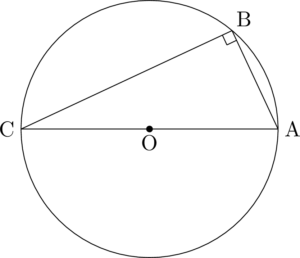



3点を通る円の方程式を簡単に求める方法とは ページ 3 大学入試数学の考え方と解法




ゼロで割ってはいけない理由を割り算の定義から考えるとこうなる アタリマエ
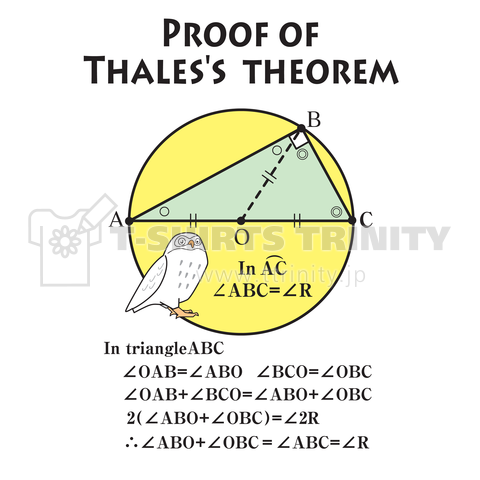



タレスの定理の証明 月と森の白フクロウ デザインtシャツ通販 Tシャツトリニティ


0 件のコメント:
コメントを投稿