石川剛郎 2年⽣ 基礎数学a,b,c,d,および,それぞれの演習 この時期までに,線形代数,位相,微分積分学の基本(=数学の基本)をしっかり⾝につけておいてください.幾何学序論やベクトル解析も(3年⽣以降の幾何の内容と関連しているので)履修するとよいです.In mathematics, integral geometry is the theory of measures on a geometrical space invariant under the symmetry group of that space In more recent times, the meaning has been broadened to include a view of invariant (or equivariant) transformations from the space of functions on one geometrical space to the space of functions on another geometrical spaceブリタニカ国際大百科事典 小項目事典 の解説 曲線, 曲面 ,さらには空間自身の研究に 微分学 と 積分学 の手法を用いる 幾何学 の一分科であって, 微分積分学 の発見と同時に始ったということができる。 しかしこれを幾何学の一分科として確立したのは C ガウス である。 B リーマン は,ガウスの曲面論を拡張して,一般次元の曲率をもつ空間の概念に達した
1
積分幾何学 pdf
積分幾何学 pdf-微分積分学 第一・第二 線形代数学 第一・第二 解析学 数学演習 第一・第二 現代数学入門A, B 代数と幾何学 応用幾何学 関数論 大学院:幾何学基礎論, 幾何学特論 (旧:現代幾何学基礎論第一, 第二)吉村洋介 積分幾何学のはなし おしまいに ぼくが積分幾何学というものに初めて触れたのは、学生時代に岩波全書で出た、木原太郎「分子間力」(岩波、1976年)を読んだ時でした。 剛体分子の第2ビリアル係数の計算を、「凸体の3基本量」(体積・表面積・"measure")を用いて行うというアイデアに感心しました。 その後、たまたま岩波の数学辞典を眺めていて



積分幾何学入門 博之 田崎 本 通販 Amazon
1 積分幾何学の基礎概念 1 1 ランダムな点 ここでは積分幾何学の基礎概念を一様にランダムな点、 の場合について説明するこれは感覚的にもわかりやす いものである 刈1 1 のように領域C。があって,内部に領域Cがある ものとする c,。現在、 ピタゴラスの定理 として知られている数学定理が、古代エジプトではすでに5000年前に経験則として知られ、縄張り師たちは345の比率で印をつけた縄を張って、畑の角の直角を取ったという 。 直角二等辺三角形におけるピタゴラスの定理の適用。 1 2 1 2 = 2 {\displaystyle {\sqrt {1^ {2}1^ {2}}}= {\sqrt {2}}} である。3,850円(税込) コマの幾何学 書影 可積分系は世紀最後の年あまりの間に,数学とその関連諸科学においてきわめて重要な位置を占めるにいたった概念であり,現在もなおその概念が拡張されて盛んに研究されている。 本書はコマの運動方程式を通じて有限次元可積分系の理論,特にその幾何学的側面を紹介するという,きわめて特色のある本である。 あらゆる
4 第1 章 曲線 k = 3, r = 1 k = 5=3, r = 1 k = 3, r = 1, l = 1 2 k = 5=3, r = 1, l = 3 2 例119 エピトロコイド(epitrochoid, がいよはいせん 外余擺線) は次の径数表示で与えられる曲線で ある。半径r の円が半径kr の円周に外接しながら滑ることなく転がるとき、動円の中心 から距離lr にある定点が描く軌跡であ世界大百科事典 第2版 積分幾何学の用語解説 古くから幾何学的確率の問題として知られた問題がある。 例えば(ユークリッド)平面におかれた二つの円周S1,S2に対して,その一方S1に交わる直線がもう一方S2にも交わる確率を求めよというものなどがそれである。価格 3,300円(税込) 復刊 積分幾何学 書影 積分幾何学の基礎を現代数学の立場から概説し,あわせて将来の発展への展望をも試みた好解説書。 『現代数学講座 積分幾何学』として1956年初版発行後,以来,長年にわたり多数の読者にご愛読いただいてまいりました。 本書は,多くの読者からの要望を受け単行本に改装し発行したものです。 mixiチェック ツイート
4 超曲面の幾何学とガウス・ボンネの定理 4 調和積分論 5 双曲幾何学入門 成績評価:講義中に課題を出し、レポートで成績評価を行う. 教科書・予備知識など: 3年生幾何学iの多様体の基礎および幾何学iiiの微分形式に関する知識を仮定する. 参考書として幾何学 iii 微分形式 / 坪井 俊 東京大学出版会, 08, isbn 幾何学 i 多様体入門 / 坪井 俊 東京大学出版会, 05, isbn 多変数解析学古典理論への現代的アプローチ / スピヴァック 東京図書, 1972, isbn可積分系(積分可能系) 四則演算,微分,不定積分,逆関数を取る,代数方程式を解く 操作を有限回合成して一般解を求められる系. (微分方程式を解く = 積分する) 線形微分方程式を解くのは易しい. 可積分な非線形微分方程式はあるか?



X132 1円 理工系 本まとめてセット 物理 数学 ファインマン 化学 半導体 電子回路 有機 微分積分 幾何学 洋書 実験 電気機械工学 の落札情報詳細 ヤフオク落札価格情報 オークフリー スマートフォン版



さのたけと ごめんなさい Chain上の積分については微分形式の引き戻しで定義できるものでした それができないと De Rham の定理の同型も書けませんね 微分形式の幾何学 P 116
統合幾何学a,大域微分幾何学–1 統合幾何学a・大域微分幾何学講義ノート この講義では前半を学部4年次科目「統合幾何学a」として多様体を,後半で大学院前期課程科目「大域微 分幾何学」としてリーマン幾何を扱う.講義は一連の内容であり,多様体の基礎からの学習を望む大学院生にフィンスラー・河口幾何学は,実は日本にも縁がある分野です. 日本の草分けは,松本誠先生,河口商次先生です. 松本先生の本,「計量微分幾何学」(裳華房)が復刊されています. この本には,フィンスラー幾何の他,河口幾何も紹介されています.微分積分学の誕生 デカルト『幾何学』からオイラー『無限解析序説』まで on Amazoncom *FREE* shipping on qualifying offers 微分積分学の誕生 デカルト『幾何学』からオイラー『無限解析序説』まで



はじめての解析学 微分 積分から量子力学まで 原岡 喜重 ブルーバックス 講談社book倶楽部
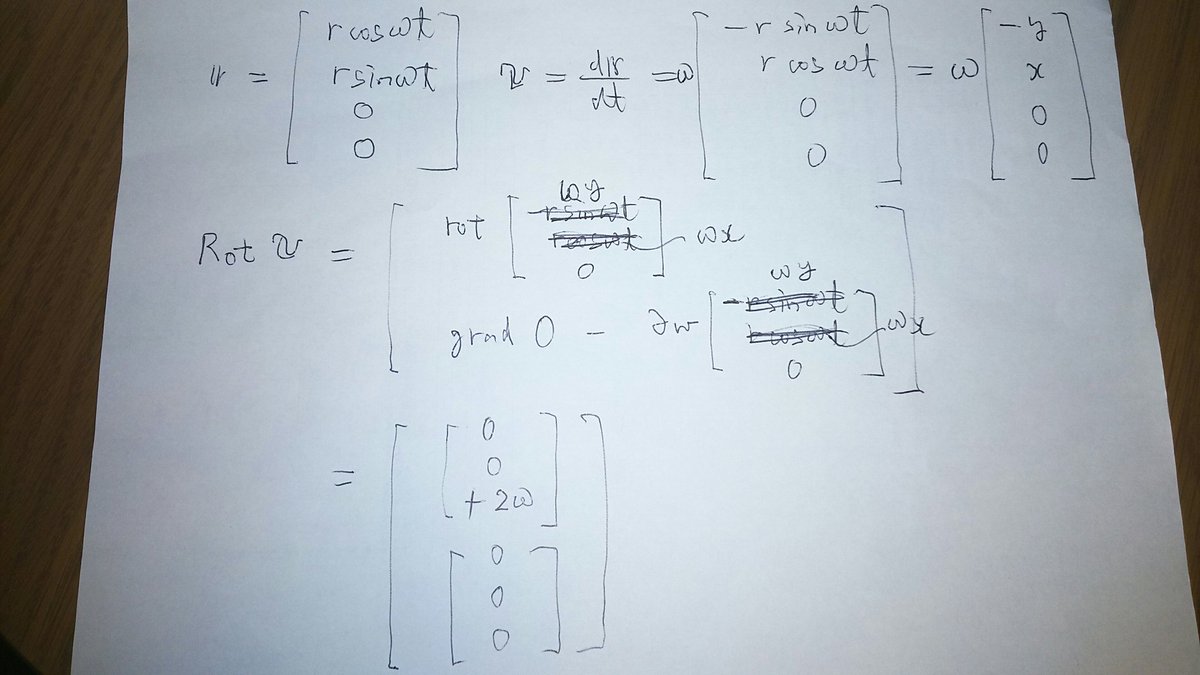


Suzy Twitter પર It Works 島田義弘著 四次元の幾何学 回転 積分 微分 プレアデス出版 の四次元ナブラを用いて簡単な四次元回転系の速度場について計算 結果は六次元ベクトルに
直しておきます 内角で書き直し (πー内角)の和+測地曲率の(線)積分+ガウス曲率の(面)積分=2𝜋 (π−π2)×304π8=2π 同じものが8枚あるので 公式も両辺8倍してみると これを8倍すると π−π2×3×804π8×8=2π×8 単位球面の面積を表す積分幾何学について(4) 腰塚武志 211 応用例3 前節の結果を応用してランダムな直線が短形の領域を よぎるとき,直線のこの領域内での長さの期待値と分散 を求めてみようこれが現実に問題とされた例として文 献16j をあげることができるもっともこの文献数学における微分幾何学(びぶんきかがく、ドイツ語 Differentialgeometrie、英語:differential geometry)とは微分を用いた幾何学の研究である。また、可微分多様体上の微分可能な関数を取り扱う数学の分野は微分位相幾何学(びぶんいそうきかがく、ドイツ語 Differentialtopologie、英語 differential topology)とよばれることがある。微分方程式の研究から自然に発生したこれらの



楽天ブックス 微分積分学の誕生 デカルト 幾何学 からオイラー 無限解析序説 まで 高瀬正仁 本



微分積分学の試練 日本評論社
等質空間の部分多様体の積分幾何学 田 崎 博 之 本稿では,Riemann等 質空問内の部分多様体の積分幾何学について解説するそ の中でも本稿の 主な話題はPoincareの 公式である Riemann等 質空間G/Kの 部分多様体MとNに ついてG上幾何学者から見た情報幾何学 記号 用語 考え方 M 多様体 高次元の曲がった空間 局所座標系を持つ TpM 接(ベクトル)空間 Mを局所線形化したベクトル空間 @xi;X 接ベクトル,接ベクトル場微分作用素(微分演算子)が接ベクトル g;h リーマン計量 曲がった空間の内積 ∇;反復積分の幾何学 河野俊丈著 (シュプリンガー現代数学シリーズ / 伊藤雄二編, 14) シュプリンガー・ジャパン, 094


1



積分の幾何学的な実体 アイコンのベクターアート素材や画像を多数ご用意 Istock
ワイヤ・ケーブルの微分幾何学 無限に細い針金のあちこちを曲げたり捻ったりすれば、 いかなる空間曲線も作れますが、 微分幾何学(differential geometry)は 空間曲線上の曲率(curvature 曲げ)と捻率(tortion 捻り)という 微分量(無限小区間に於ける変化量)を使って、 空間曲線や空間曲面を解析する手幾何学いろいろ, 可積分系もいろいろGeometry, it's a secret ingredient that makes integrable system theory interesing for us井ノ口 順一 (Junichi Inoguchi) 宇都宮大学教育学部 (Utsunomiya University) In this 概要 talk, I would like to exhibit some derived from integrable systems nonEulidean plane geometries はじめに ソリ積分幾何学 交叉積分公式 論文、21とそれに続く複素射影空間の積分幾何学に関する研究で、Kahler角度や多重Kahler角度による積分公式を求めました。 08年の正月にそれらの積分公式を拡張した論文が著者から送られてきて、凸体の幾何学と密接な関係があることを知りました。 これは大変なことになっていると気付き、その方面の勉強を始めて凸体の交叉積分公式


1



微分積分学の誕生 Sbクリエイティブ
この記事では,リー微分を理解するのに必要な流れの具体例をいくつか見ます. 記法としては,中原幹夫先生の理論物理学のための幾何学とトポロジーiのものを採用します. 以下では二次元平面上の事を考え,ベクトル場を で,積分曲線を とします.リーマン幾何学において、リーマン幾何学の基本定理(fundamental theorem of Riemannian geometry)は、任意のリーマン多様体(あるいは、擬リーマン多様体)には、捩れのない計量接続が一意的に存在するという定理である。 この接続は、与えられた計量のレヴィ・チヴィタ接続(LeviCivita connection)と呼ば算数から微積分への橋わたしをする代数の名著 第2巻 わかる三角法 苦心の例題・問題とともに「わかる」を第一の目的とした 第3巻 わかる幾何学 だれでも気持よくわかる・読んで頭を悩まさない 第4巻 わかる立体幾何学



微分積分学の誕生 デカルト 幾何学 からオイラー 無限解析序説 まで 漫画 無料試し読みなら 電子書籍ストア ブックライブ



微分積分学の史的展開 ライプニッツから高木貞治まで 高瀬 正仁 講談社book倶楽部
積分幾何学 古くから幾何学的確率の問題として知られた問題がある。 例えば(ユークリッド)平面におかれた二つの円周 S1 , S2 に対して微分 形式 の 幾何 学 pdf 1 微分形式の幾何学への入門 ユークリッド空間の領域上の微分形式とその外微分 ユークリッド空間Rn の領域D で定義された1次微分形式ω は,座標関 数x1,··· ,xn を用いて ω = a1dx1 ···andxn と表される.ここで,a1,··· ,an はD で定義されたC∞ 関数である.これは微分形式の積分の章で幾何学的に翻訳される ωをR^nの開集合U上の閉k形式としΦをU内のC^2級(k+1)鎖とすれば ∫_∂Φ ω = 0, ωをR^nの開集合U上の完全k形式とする このときΦ, ΨがC^2級の鎖で∂Φ=∂Ψなら ∫_Φ ω = ∫_Ψ ω



M2uegelibytihm



単行本 高瀬正仁 微分積分学の誕生 デカルト 幾何学 からオイラー 無限解析序説 までの通販はau Pay マーケット Hmv Books Online
物理学から幾何学へ—モジュライと径路積分 中村郁 1 八重洲口, 3 月 05 年3 月末,八重洲口の近くで大学1 年の クラス会があった.久しぶりに東京に出た私のた めに,友人数人がわざわざ集まってくれたのであ る.会社の社長もいれば,大学卒業後もう微分積分・線形代数 線形代数 微分積分 解析学・応用解析 確率・統計 or 代数学 幾何学 集合・位相 応用数学 電子計算機・情報 分野別一覧 書名五十音別 isbn順一覧 シリーズ一覧 電子書籍 復刊書籍一覧 復刊リクエスト 書評掲載本 目録請求 出版書誌微分幾何学はもともと、3次元ユークリッド空間のなめらか(微分可能)な曲線や曲面上の1点の近傍の性質を微分学を用いて論じるものでした。 これはオイラー(LEuler 1707~17年)やモンジュ(GMonge 1746~1818年)に始まり、最終的にガウス(CFGauss 1777


2



ヤフオク 微分幾何学 の落札相場 落札価格


1


Dimension Of Motoo Tange



ヤフオク 微分幾何学 の落札相場 落札価格



書籍紹介 微分積分学 岩堀長慶 編 数学



数学 物理に関する本 まとめて112冊 大量セット 岩波書店 微分積分 幾何学 整数 代数 複素数 電磁気学 の落札情報詳細 ヤフオク落札価格情報 オークフリー スマートフォン版


Dimension Of Motoo Tange



書籍紹介 大学演習 微分積分学 三村征雄 編 数学



国際研究集会 代数幾何学と可積分系 神戸16 国立大学法人 神戸大学 Kobe University



コマの幾何学 可積分系講義 Michele Audin 著 高崎 金久 訳 共立出版



ヤフオク 数学 物理学に関する本 まとめて80冊大量セット



復刊 積分幾何学 栗田 稔 本 通販 Amazon


1



ページサンプル閲覧 達人出版会



微分積分学の誕生 デカルト 幾何学 からオイラー 無限解析序説 まで 高瀬正仁 とね日記



Integrable Systems And Algebraic Geometry Volume 1 Donagi Ron Edt Shaska Tony Edt 電子版 紀伊國屋書店ウェブストア オンライン書店 本 雑誌の通販 電子書籍ストア



ブルーバックス Blue Backs 数学 物理 関連まとめて104冊 微分 積分 幾何学 統計 トポロジー ファインマン 代数学 解析学 大量セット 40 の落札情報詳細 ヤフオク落札価格情報 オークフリー スマートフォン版



河野 俊丈 Toshitake Kohno 反復積分の幾何学 シュプリンガー現代数学シリーズ第14巻 書籍等出版物 Researchmap



X466 1円 数学本まとめてセット 確率 微分積分 幾何学 行列 楕円 円形 集合 曲線 関数 教育 ベクトル 解析 計算 問題 代数 係数 多項式 の落札情報詳細 ヤフオク落札価格情報 オークフリー スマートフォン版


大学数学のロードマップ 分野一覧と学ぶ順序 趣味の大学数学



英語数学洋書 Motivic Integration And Its Interactions With Model Theory And Non Archimedean Geometry Volume Ii モチーフ積分とそのモデル理論および非アルキメデス的幾何学との相互作用 第2巻 Edited By Raf Cluckers 古本 中古本 古書籍の通販は 日本の



ブルーバックス Blue Backs 数学 物理 関連まとめて104冊 微分 積分 幾何学 統計 トポロジー ファインマン 代数学 解析学 大量セット 40 の落札情報詳細 ヤフオク落札価格情報 オークフリー スマートフォン版


2



積分幾何学入門 博之 田崎 本 通販 Amazon



X466 1円 数学本まとめてセット 確率 微分積分 幾何学 行列 楕円 円形 集合 曲線 関数 教育 ベクトル 解析 計算 問題 代数 係数 多項式 の落札情報詳細 ヤフオク落札価格情報 オークフリー スマートフォン版



コマの幾何学 可積分系講義の通販 michele audin 高崎 金久 紙の本 Honto本の通販ストア



理論物理学のための 幾何学とトポロジー1 日本評論社


京都大学大学院情報学研究科数理工学専攻



数学関連本13冊まとめ 微分積分 リーマン幾何学 相対性理論 超複素数入門 電磁気学等 数学 売買されたオークション情報 Yahooの商品情報をアーカイブ公開 オークファン Aucfan Com



F X F X E X 型の積分の公式 Canada S Windview



幾何学 Wikipedia



数学に関する本 まとめて 冊セット ガロア トポロジー リーマン 代数 微分積分 幾何学 新初等数学講座 他 Ba の落札情報詳細 ヤフオク落札価格情報 オークフリー スマートフォン版



部分積分法の応用 Xのn次式と対数関数の積の積分 Canada S Windview
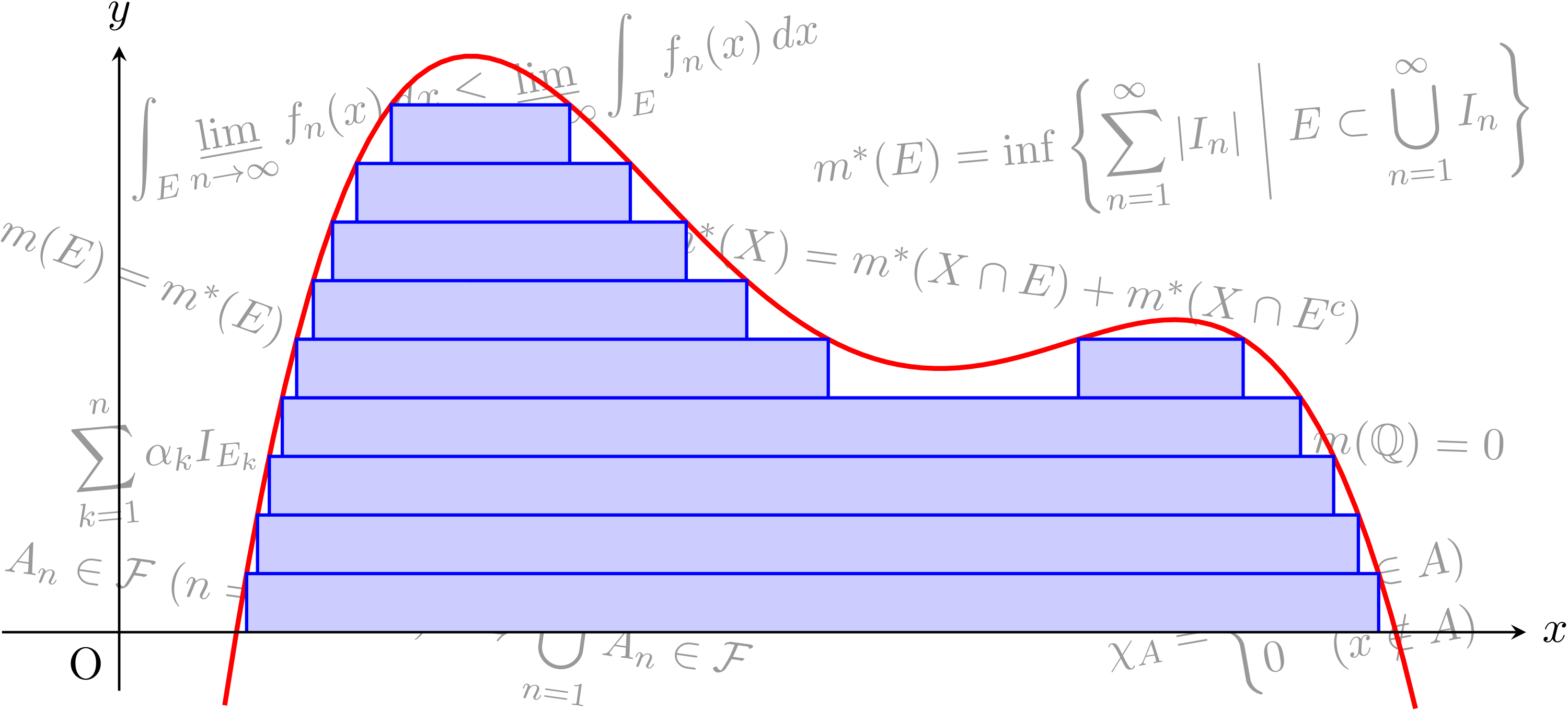


積分の歴史 ルベーグ積分までの道のり 数学 統計教室の和から株式会社



基礎 解析幾何学の中古 未使用品を探そう メルカリ



数理科学 2013年2月号 特集 量子化 の発想 可積分系から幾何学まで 白石潤一 A ザブロージン 木村嘉之 髙木寛通 池田岳 A N キリロフ 野海正俊 M フィンケルベルグ 戸松玲治 特集 古本 中古本 古書籍の通販は 日本の古本屋 日本の古本屋



微分幾何学の値段と価格推移は 48件の売買情報を集計した微分幾何学の価格や価値の推移データを公開



積分幾何学 その2



測度 確率 ルベーグ積分 応用への最短コース 漫画 無料試し読みなら 電子書籍ストア ブックライブ



ページサンプル閲覧 達人出版会



スタイリッシュな 3 D パターン 背景紙で穴あきの効果が好き 幾何学的なデザイン 穴あき紙厚の積分 のイラスト素材 ベクタ Image


積分幾何学のはなし 直線の測度



数学に関する本 まとめて 冊セット ガロア トポロジー リーマン 代数 微分積分 幾何学 新初等数学講座 他 Ba の落札情報詳細 ヤフオク落札価格情報 オークフリー スマートフォン版



ヤフオク 微分幾何学 数学 の中古品 新品 古本一覧



楽天ブックス 反復積分の幾何学 河野 俊丈 本



演習 重積分 Youtube



積分幾何学入門 博之 田崎 本 通販 Amazon



新装版 対話 微分積分学 数学解析への誘い 株式会社 現代数学社



書泉グランデmath 営業時間11時 時 No Twitter 好評発売中 曲面と可積分系 井ノ口順一 著 しゃぼん玉を数学的に表現した 平均曲率一定曲面 を中心に 曲面の幾何学の基礎を学ぶ 解ける 積分できる 偏微分方程式の研究である無限可積分系と微分幾何学が



ヨドバシ Com 四次元の幾何学 回転 積分 微分 単行本 通販 全品無料配達



微分積分学ii 15 Courses


受験生のために 数学教育室


積分幾何学のはなし ビュフォンの針



色を測定する幾何学的条件 株式会社 村上色彩技術研究所



アルケミスト双書 イスラム芸術の幾何学 天上の図形を描く 漫画 無料試し読みなら 電子書籍ストア ブックライブ


大学数学の幾何学の積分の問題です 2行目から3行目にかけてどの様な計算を行 Yahoo 知恵袋
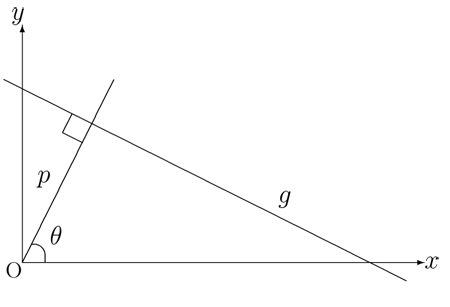


積分幾何学とは何 Weblio辞書



Lohaco 微分積分学の誕生 デカルト 幾何学 からオイラー 無限解析序説 まで 高瀬正仁 数学 Bookfan For Lohaco



抽象的な幾何学模様 モダンな白黒背景 垂直方向の積分と灰色のフラット のイラスト素材 ベクタ Image



明倫館書店 反復積分の幾何学



曲直瀬おめが 幾何学vtuber リーマン多様体における積分とホッジの定理 についてのノートを書きました 特色としては 必ずしも向き付け可能とは限らない リーマン多様体における関数の積分の定義および発散定理の証明を書いたことだと思います


Www Ap Graduate Tsukuba Ac Jp Wp Content Themes Twentytwelve Pdf Pas First Research Pdf



無料の数学プロブレムソルバーが まるで数学の家庭教師のように ステップバイステップの説明とともにあなたの代数 幾何学 三角関数 微分積分の宿題の問題を解決します 微分積分 代数 分数



積分計算を駆使して都市を測る 応用のための積分幾何学 図形の測度 道路網 市街地 施設配置 発行 株式会社インプレスホールディングスのプレスリリース



英語数学洋書 Motivic Integration And Its Interactions With Model Theory And Non Archimedean Geometry Volume Ii モチーフ積分とそのモデル理論および非アルキメデス的幾何学との相互作用 第2巻 Edited By Raf Cluckers 古本 中古本 古書籍の通販は 日本の



数学に関する本 まとめて 冊セット ガロア トポロジー リーマン 代数 微分積分 幾何学 新初等数学講座 他 Ba の落札情報詳細 ヤフオク落札価格情報 オークフリー スマートフォン版



01 同梱不可 数学関連本まとめ売り約40冊大量セット 幾何学 公式 計算 証明 群論 関数 数列 微分積分 フーリエ級数 位相 確率 A 日本代購代bid第一推介 Funbid


積分幾何学のはなし 図形と交わる直線の測度


幾何学 Wikipedia
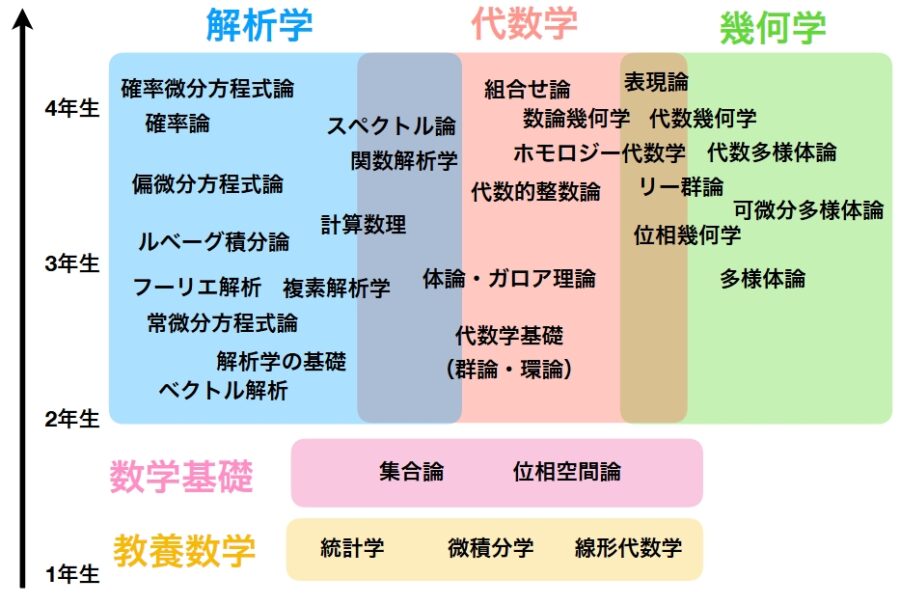


大学数学のロードマップ 分野一覧と学ぶ順序 趣味の大学数学



X132 1円 理工系 本まとめてセット 物理 数学 ファインマン 化学 半導体 電子回路 有機 微分積分 幾何学 洋書 実験 電気機械工学 の落札情報詳細 ヤフオク落札価格情報 オークフリー スマートフォン版


朝倉書店 曲面と可積分系


朝倉書店 確率幾何解析



コーシーの積分公式の利用と最大値の原理の証明 身勝手な主張



微分積分学の誕生 高瀬 正仁 著 文 Sbクリエイティブ 版元ドットコム



セシル على تويتر 博論作成よりhitchin可積分系pdf作成の方が捗ってる



積分幾何学入門 博之 田崎 本 通販 Amazon



数学 物理学に関する本 まとめて80冊大量セット 高木貞治 ベクトル 微分 積分 代数 解析学 幾何学 関数 トポロジー 群論 Ba 日本代購代bid第一推介 Funbid



合成関数の積分の公式 Canada S Windview



積分計算を駆使して都市を測る 応用のための積分幾何学 図形の測度 道路網 市街地 施設配置 発行 ニコニコニュース



ヤフオク 微分幾何学の中古品 新品 未使用品一覧



積分の幾何学的なエンティティです アイコンのストックフォトや画像を多数ご用意 Istock



積分幾何学入門 博之 田崎 本 通販 Amazon



復刊 積分幾何学 栗田 稔 本 通販 Amazon



ヤフオク 積分方程式 数学 自然科学と技術 の落札相場 落札価格



数学 物理に関する本 まとめて112冊 大量セット 岩波書店 微分積分 幾何学 整数 代数 複素数 電磁気学 の落札情報詳細 ヤフオク落札価格情報 オークフリー スマートフォン版



Lohaco 四次元の幾何学 回転 積分 微分 島田義弘 数学 Bookfan For Lohaco


ときわ台学 解析学 リーマン積分



X466 1円 数学本まとめてセット 確率 微分積分 幾何学 行列 楕円 円形 集合 曲線 関数 教育 ベクトル 解析 計算 問題 代数 係数 多項式 の落札情報詳細 ヤフオク落札価格情報 オークフリー スマートフォン版


0 件のコメント:
コメントを投稿